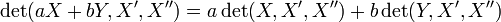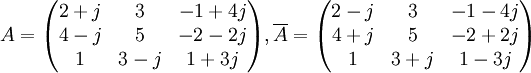domingo, 17 de octubre de 2010
en que se aplican los temas vistos en clase
3.1 Definición de matriz, notación, orden.
3.2 Operaciones con matrices ( suma, resta, producto, producto de un escalar por una matriz).
3.3 Clasificación de las matrices triangular superior, triangular inferior, diagonal, escalar, identidad, potencia, periódica, nilpotente, idempotente, involutiva, transpuesta, simétrica, antisimétrica, compleja, conjugada, hermitiana, antihermítiana, ortogonal.
3.4 Cálculo de la inversa de una matriz.
3.5 Definición de determinante de una matriz.
3.6 Propiedades de los determinantes.
3.7 Inversa de una matriz cuadrada a través de la adjunta.
3.8 Solución de un sistema de ecuaciones lineales a través de la inversa.
3.9 Solución de un sistema de ecuaciones lineales por la regla de Cramer.
3.10 Aplicación de matrices y determinantes.
como todo trata de matrices se puede decir que su uso es para resolver sistemas de ecuaciones, para solucionar problemas de cualquier tipo que se presenten en el campo laboral, te abren campo a varias posibilidades y te dan varias alternativas para ver si el problema tiene o no solución.
información proporcionada por:
ing. Franco Garduño
puesto de confianza en el sistema estatal de informatica
3.2 Operaciones con matrices ( suma, resta, producto, producto de un escalar por una matriz).
3.3 Clasificación de las matrices triangular superior, triangular inferior, diagonal, escalar, identidad, potencia, periódica, nilpotente, idempotente, involutiva, transpuesta, simétrica, antisimétrica, compleja, conjugada, hermitiana, antihermítiana, ortogonal.
3.4 Cálculo de la inversa de una matriz.
3.5 Definición de determinante de una matriz.
3.6 Propiedades de los determinantes.
3.7 Inversa de una matriz cuadrada a través de la adjunta.
3.8 Solución de un sistema de ecuaciones lineales a través de la inversa.
3.9 Solución de un sistema de ecuaciones lineales por la regla de Cramer.
3.10 Aplicación de matrices y determinantes.
como todo trata de matrices se puede decir que su uso es para resolver sistemas de ecuaciones, para solucionar problemas de cualquier tipo que se presenten en el campo laboral, te abren campo a varias posibilidades y te dan varias alternativas para ver si el problema tiene o no solución.
información proporcionada por:
ing. Franco Garduño
puesto de confianza en el sistema estatal de informatica
representacion grafica de la determinante de una matriz
El cálculo de áreas y volúmenes bajo forma de determinantes en espacios euclídeos aparecen como casos particulares de una noción más general de determinante. La letra mayúscula D (Det) se reserva a veces para distinguirlos.
Determinante de dos vectores en el plano euclídeo
Sea P el plano euclídeo. El determinante de los vectores X y X' se obtiene con la expresión analíticaPropiedades
- El valor absoluto del determinante es igual a la superficie del paralelogramo definido por X y X' (Xsinθ es en efecto la altura del paralelogramo, por lo que A = Base × Altura).
- El determinante es nulo si y sólo si los dos vectores son colineales (el paralelogramo se convierte en una línea).
- Su signo es estrictamente positivo si y sólo si la medida del ángulo (X, X ') se encuentra en ]0,π[.
- La aplicación del determinante es bilineal: la linearidad respecto al primer vector se escribe
El dibujo corresponde a un caso particular de la fórmula de bilinealidad ya que las orientaciones han sido elegidas de manera que las áreas tengan el mismo signo, aunque ayuda a comprender el contenido geométrico.
Generalización
Es posible definir la noción de determinante en un plano euclídeo orientado con una base ortonormal directa B utilizando las coordenadas de los vectores en esta base. El cálculo del determinante da el mismo resultado sea cual sea la base ortonormal directa elegida para el cálculo.Determinante de tres vectores en el espacio euclídeo
Sea E el espacio euclídeo orientado de dimensión 3. El determinante de tres vectores de E se da porPropiedades
- El valor absoluto del determinante es igual al volumen de paralelepípedo definido por los tres vectores.
- El determinante es nulo si y sólo si los tres vectores se encuentran en un mismo plano (paralelepípedo "plano").
- La aplicación determinante es trilineal: sobre todo
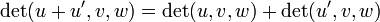 .
.
tipos de matrices (ejemplos)
Matriz cuadrada
Matriz triangular
superior
inferior 
Matriz diagonal

Matriz escalar
Matriz identidad
Matriz indempotente
Matriz transpuesta

Matriz involutiva
Matriz simetrica
Matriz antisimetrica
 = >
= > 
Matriz compleja
Matriz conjugada
Matriz hermitiana
Matriz antihermitiana
Matriz ortogonal
Suscribirse a:
Entradas (Atom)